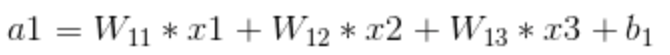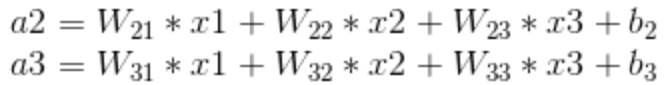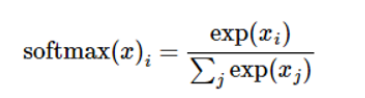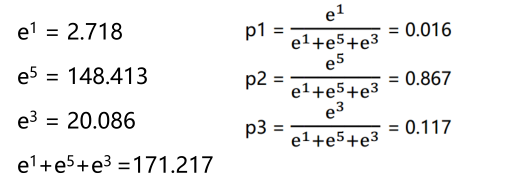主要来源和参考的资料为:炼数成金视频《深度学习框架TensorFlow学习与应用》以及补充了一些网上的博文内容。
视频目录:
第 1周 Tensorflow简介,Anaconda安装,Tensorflow的CPU版本安装
第 2周 Tensorflow的基础使用,包括对图(graphs),会话(session),张量(tensor),变量(Variable)的一些解释和操作
第 3周 Tensorflow线性回归以及分类的简单使用
第 4周 softmax,交叉熵(cross-entropy),dropout以及Tensorflow中各种优化器的介绍
第 5周 卷积神经网络CNN的讲解,以及用CNN解决MNIST分类问题
第 6周 使用Tensorboard进行结构可视化,以及网络运算过程可视化
第 7周 递归神经网络LSTM的讲解,以及LSTM网络的使用
第 8周 保存和载入模型,使用Google的图像识别网络inception-v3进行图像识别
第 9周 Tensorflow的GPU版本安装。设计自己的网络模型,并训练自己的网络模型进行图像识别
第10周 使用Tensorflow进行验证码识别
第11周 Tensorflow在NLP中的使用(一)
第12周 Tensorflow在NLP中的使用(二)说明:实际第 5 周讲的是 Tensorborad 结构可视化,第 6 周讲的是 CNN。修正:下载链接里的文件夹顺序,我已修正。
(1) 在线观看:
- YouTube:tensorflow教程(十课)
- 或 B 站:《深度学习框架TensorFlow学习与应用》
(2) 下载:
-
《深度学习框架Tensorflow学习与应用》(含视频+代码+课件,视频总时长:13小时31分钟)
链接: https://pan.baidu.com/s/16OINOrFiRXbqmqOFjCFzLQ 密码: 1a8j
-
《深度学习框架Tensorflow学习与应用[只有videos-720p]》(该份资料只有视频文件)
链接: https://pan.baidu.com/s/1oQLgWFEBsVrcKJN4swEdzg 密码: i3e2
其他学习视频(觉得有必要可以去看看):
- 油管视频:TF Girls 修炼指南 、或 B 站观看: TF Girls 修炼指南
- 油管视频:51CTO视频 深度学习框架-Tensorflow案例实战视频课程、或 B 站观看:深度学习框架-Tensorflow案例实战视频课程
相关资料:
- 郑泽宇/顾思宇:《Tensorflow:实战Google深度学习框架》 出版时间 2017-2-10
- 官方维护的书中的 TensorFlow 不同版本的示例程序仓库:https://github.com/caicloud/tensorflow-tutorial;
- GitHub 有人写了笔记:TensorFlow_learning_notes
- 黄文坚/唐源:《TensorFlow实战》 出版时间 2017-2-1
- 掘金翻译:TensorFlow 最新官方文档中文版 V1.10
- 极客学院:TensorFlow 官方文档中文版
- TensorFlow 官方文档中文版
《深度学习框架Tensorflow学习与应用》笔记:
- 01-Tensorflow简介,Anaconda安装,Tensorflow的CPU版本安装
- 02-Tensorflow的基础使用,包括对图(graphs),会话(session),张量(tensor),变量(Variable)的一些解释和操作
- 03-Tensorflow线性回归以及分类的简单使用
- 04-softmax,交叉熵(cross-entropy),dropout以及Tensorflow中各种优化器的介绍
- 05-使用Tensorboard进行结构可视化,以及网络运算过程可视化
- 06-卷积神经网络CNN的讲解,以及用CNN解决MNIST分类问题
- 07-递归神经网络LSTM的讲解,以及LSTM网络的使用
- 08-保存和载入模型,使用Google的图像识别网络inception-v3进行图像识别
- 09-Tensorflow的GPU版本安装。设计自己的网络模型,并训练自己的网络模型进行图像识别
- 10-使用Tensorflow进行验证码识别
- 11-Tensorflow在NLP中的使用(一)
- 12-Tensorflow在NLP中的使用(二)
1、在 03-Tensorflow线性回归以及分类的简单使用 中(二)节开始以手写数字识别 MNIST 例子来讲解,关于 MNIST 的内容还可以看看该 README 下面的。
2、发现了问题:在 04-softmax,交叉熵(cross-entropy),dropout以及Tensorflow中各种优化器的介绍 中(三)节开始的代码4-1交叉熵.py,可以注意到如下代码:
# 创建一个简单的神经网络
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
prediction = tf.nn.softmax(tf.matmul(x, W) + b)
# 二次代价函数
# loss = tf.reduce_mean(tf.square(y-prediction))
# 这里使用对数释然代价函数tf.nn.softmax_cross_entropy_with_logits()来表示跟softmax搭配使用的交叉熵
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=prediction))我觉得这里是有问题的,问题在哪呢?先看【TensorFlow】tf.nn.softmax_cross_entropy_with_logits的用法该文,可以了解到 tf.nn.softmax_cross_entropy_with_logits 函数的 logits 参数传入的是未经过 softmax 的 label 值。
import tensorflow as tf
#our NN's output
logits=tf.constant([[1.0,2.0,3.0],[1.0,2.0,3.0],[1.0,2.0,3.0]]) #step1:do softmax
y=tf.nn.softmax(logits)
#true label
y_=tf.constant([[0.0,0.0,1.0],[0.0,0.0,1.0],[0.0,0.0,1.0]])
#step2:do cross_entropy
cross_entropy = -tf.reduce_sum(y_*tf.log(y)) 两步可以用这一步代替:
#do cross_entropy just one step
cross_entropy2=tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(logits, y_))#dont forget tf.reduce_sum()!! 但prediction = tf.nn.softmax(tf.matmul(x, W) + b)这里的 prediction 已经经历了一次 softmax,然后又经过了 tf.nn.softmax_cross_entropy_with_logits 函数,这相当于经过两个 softmax 了(虽然大的值的概率值还是越大,这点上倒是没影响。)
关于 softmax_cross_entropy_with_logits,这篇文章也有提到【TensorFlow入门】:
这个函数内部自动计算 softmax 函数,然后在计算代价损失,所以logits必须是未经 softmax 处理过的函数,否则会造成错误。
注1:好像后面的笔记中程序代码都是这样的,我觉得可能视频讲解老师没注意到这点问题。另外,在该文 06-卷积神经网络CNN的讲解,以及用CNN解决MNIST分类问题 的笔记中,我也记录了该问题。
注2:对 softmax、softmax loss、cross entropy 不了解,可以看下网上该文 卷积神经网络系列之softmax,softmax loss和cross entropy的讲解,讲解地非常清楚。【荐】
另外,关于在 TensorFlow 中有哪些损失函数的实现呢?看看该文:tensorflow API:tf.nn.softmax_cross_entropy_with_logits()等各种损失函数
3、在 05-使用Tensorboard进行结构可视化,以及网络运算过程可视化 该文可以学习到:
- 用例子演示如何使结构的可视化
- 参数细节的可视化,绘制各个参数变化情况
- 补充内容:可视化工具 TensorBoard 更多使用和细节★(这部分会不断补充和更新的…)
4、在 06-卷积神经网络CNN的讲解,以及用CNN解决MNIST分类问题 该文可以学习到:
- 卷积神经网络 CNN(包括局部感受野、权值共享、卷积、池化)
- 补充内容:参数数量的计算(以 LeNet-5 为例子)
- 补充内容:TensorFlow 中的 Padding 到底是怎样的?★ (这个认真看下~)
- 补充内容:TensorFlow 中的 Summary 的用法
-
通过该文重点体会下网络结构卷积、池化过程,feature map 以及深度的变化。
如果不清楚,可以看下该文【从AlexNet理解卷积神经网络的一般结构】,现摘入部分内容:
CNN 中的卷积层操作与图像处理中的卷积是一样的,都是一个卷积核对图像做自上而下,自左而右的加权和操作,不同指出在于,在传统图像处理中,我们人为指定卷积核,比如 Soble,我们可以提取出来图像的水平边缘和垂直边缘特征。而在 CNN 中,卷积核的尺寸是人为指定的,但是卷积核内的数全部都是需要不断学习得到的。比如一个卷积核的尺寸为
3×3×3,分别是宽,高和厚度,那么这一个卷积核中的参数有 27 个。在这里需要说明一点:- 卷积核的厚度=被卷积的图像的通道数
- 卷积核的个数=卷积操作后输出的通道数
这两个等式关系在理解卷积层中是非常重要的!!举一个例子,输入图像尺寸
5×5×3(宽/高/通道数),卷积核尺寸:3×3×3(宽/高/厚度),步长:1,边界填充:0,卷积核数量:1。用这样的一个卷积核去卷积图像中某一个位置后,是将该位置上宽 3,高 3,通道 3 上 27 个像素值分别乘以卷积核上 27 个对应位置的参数,得到一个数,依次滑动,得到卷积后的图像,这个图像的通道数为 1(与卷积核个数相同),图像的高宽尺寸如下公式:所以,卷积后的图像尺寸为:
3×3×1(宽/高/通道数) -
该文讲解的挺全面的,值得一看。现摘入其中部分内容:
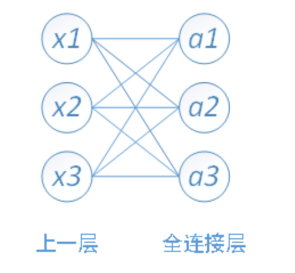
全连接层,顾名思义,指的是这一层的每个节点都跟上一层的全部节点有连接。
比如图中全连接层的节点 a1 与上一层的所有节点 x1、x2、x3 有联系,a2 也与上一层的所有节点有联系,就这样,少一个也不行。因此解释全连接层的时候,图就是上面这样一个网状结构。
假设 x1,x2,x3 是全连接层的输入值,那么在全连接层的 a1 可以表示为以下的形式。
从这个公式可以看出,a1 与 x1,x2,x3 都有联系,只是输入节点的权重值不同。同理,a2 和 a3 也可以表示为以下的形式。
由此就可以从数学层面去理解什么叫全连接层,但是这个全连接层在实际应用中表示得意义是什么呢,简单来说,它可以作为一个分类网络,还是上面那个图,输入层是 3 个值,全连接层是 3 个节点,就代表这个全连接层可以把上一层的特征值分类为三种特征。当然,输入层和全连接层的节点数并不一定相同,比如下面这个结构。
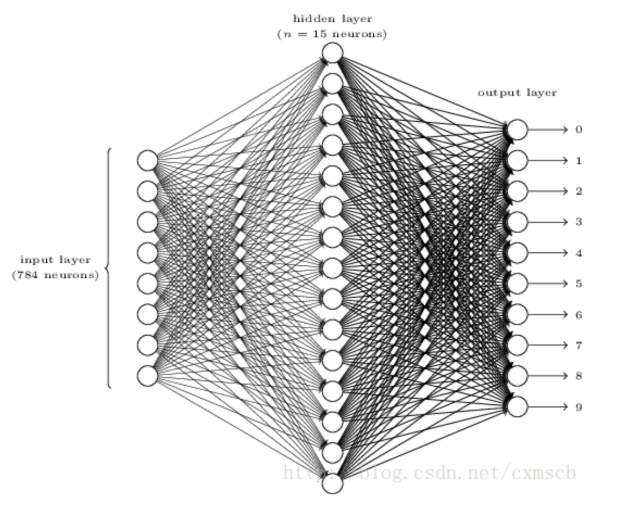
最后的全连接层是 10 个节点,全连接层的上一层是 15 个特征值,这样就把 15 个特征值归类为 10 种特征。举例来说,比如输出的 15 个特征标记位 t1-15,而 t1,t3,t5 三种特征可以认为都属于某一种输出 o1。而 t2,t6 两种特征可以认为属于输出 o2,以此类推,就可以把 15 个特征分类为 10 个输出。
前面提到的 MNIST 问题中,全连接层有两层,第一层是 1024 个节点,第二层是 10 个节点。一般情况下,最靠近用户的输出层就是用户所期待的结果类别数,MNIST 问题中,用户期待的输出是 0-9 一共 10 个数字也就是 10 种类别,所以第二层全连接层是 10 个节点。再往前看,卷积层在每一个像素点上提取 64 个特征值,所以整个图片可以有
高x宽x64个特征值,也就是7x7x64个特征,第一个全连接层是 1024 个节点,表示希望这个网络将这 7764 个特征归类为 1024 个分类。至于为什么第一个连接层是 1024 个节点,是一个经验值的问题,这个节点的个数是可以调整的,后面会讲到全连接层对模型体积的影响,也会再说到这个经验值的问题。那么全连接层是如何分类的,一起来看一下。(剩下内容略……)
个人补充:关于 softmax 函数。
我们知道 MNIST 的结果是 0-9,我们的模型可能推测出一张图片是数字 9 的概率是 80%,是数字 8 的概率是 10%,然后其他数字的概率更小,总体概率加起来等于 1。这是一个使用 softmax 回归模型的经典案例。softmax 模型可以用来给不同的对象分配概率。
比如输出结果为[1, 5, 3]:
softmax 多用于多分类神经网络输出。
-
通过该文重点体会下神经网络最后是如何做到数字分类的。
参考「机器之心」编译文章:
本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。使用者可以对本创作进行转载、节选、混编、二次创作,但不得运用于商业目的,且使用时须进行署名,采用本创作的内容必须同样采用本协议进行授权。
欢迎关注公众号:一个程序员的随想