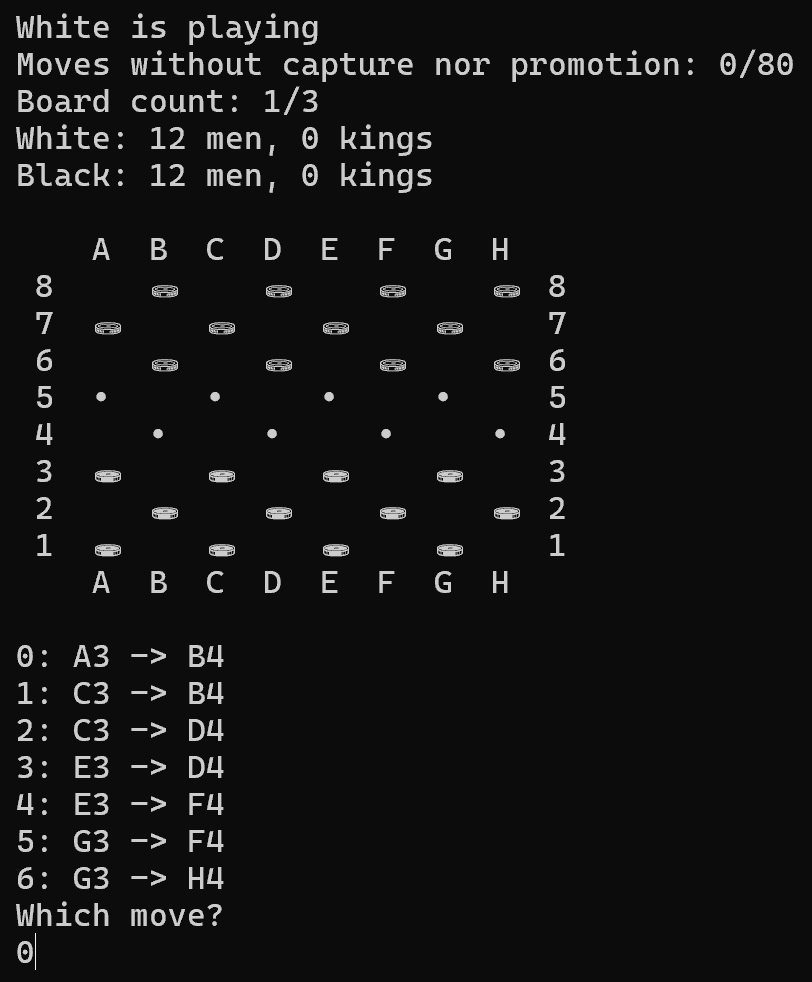
A checkers (or draughts) game with several AI algorithms available, written in Rust (and a bit of CUDA).
Rules: English draughts
# Clone the repository:
git clone git@github.com:rreemmii-dev/Checkers-AI.git
cd Checkers-AIEnsure you have cargo installed.
There are several versions available, according to the tool you want to use to compute the neural networks.
Requires no additional installation, but probably the slowest version.
cargo run --release --features baseTo use OpenBLAS, a BLAS running on CPUs.
cargo run --release --features openblasTo use CUDA and cuBLAS, a BLAS running on NVIDIA GPUs.
cargo run --release --features cublasThere are currently 2 possible AI algorithms. The first one is a simple one, using a negamax search and alpha-beta pruning. The second one is a more complex one, using a neural network.
The idea is to run several negamax searches using alpha–beta pruning, each in a different thread.
Thus, the AI runs in two parts:
-
A shallow multithreaded depth-first search (DFS), in which the AI goes about 2 moves deep.
-
A negamax search with alpha-beta pruning at the end of each branch of the initial DFS.
As the negamax exploration is run with a limited depth, a way to compute the score of a board is required.
First, a score has to be chosen for each piece. It depends on the piece type (man or king) and its position on the board. For exemple, men near promotion line and kings near the middle of the board are more valuable.
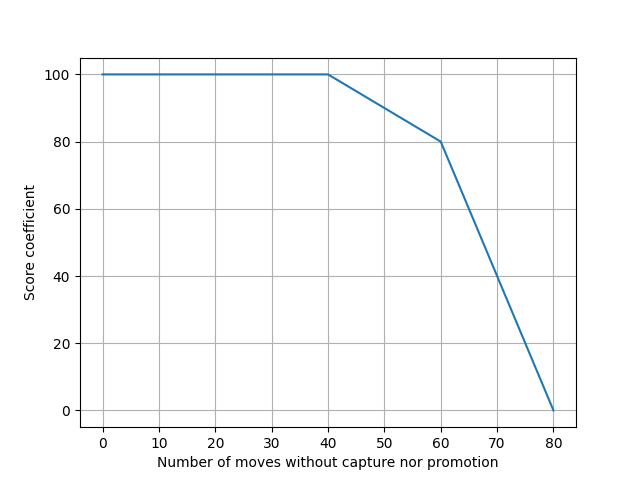
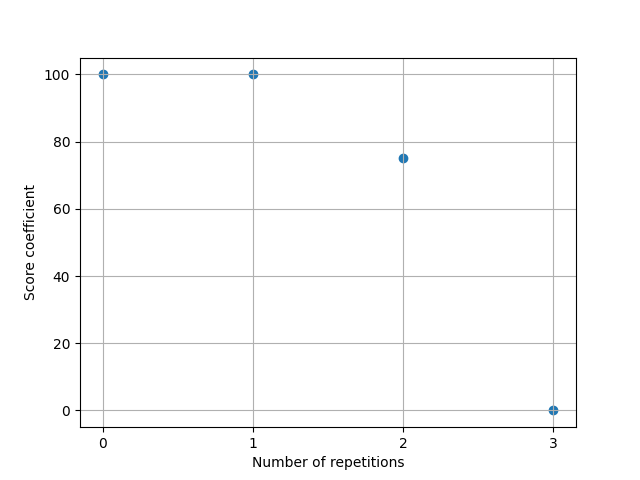
Then, a coefficient has to be chosen, representing how close the game is to become a draw (either by 3 repetitions, or by playing 2 * 40 moves without capture nor promotion). A coefficient of 50 (out of 100) reduces players' effective score by half, bringing them closer to a draw. The following functions where chosen (rather arbitrarily):
The goal is to use a neural network to compute boards scores at the end of alpha-beta searches, instead of using a rather arbitrarily chosen function.
A multilayer perceptron is used. Its input is an array of 130 values: 4 values * 32 squares to know which piece is in the square (if any), then 1 value for the number of moves since the last capture and 1 value for the number of repetitions. Its output is a score between 0 and 1, the bigger the better for the current player.
Everything related to the implementation of the neural network can be found in src/players/neural_network/neural_network.md.
The goal is to ultimately have a bot playing without any prior knowledge other than the checkers rules. Thus, there is no supervised learning: the bot learns by playing against itself.
Currently, there are 4 different neural networks, playing against each other and learning from these games. However, as the learning rate is difficult to choose, an evolutionary algorithm is used. There are 7 groups having a different learning rate each. Then, after some time (about 1h), the best group among the 7 is chosen. The winning group is cloned in 7 groups, each having the exact same neural networks, but slightly different learning rates, all chosen near the value of the winning group.
Below are explained some methods used to improve performance.
Bitboards are a way to avoid iterating over each square, for exemple while searching for possible moves.
3 bitboards are enough to store the whole board: one for white pieces, one for black pieces and one for both white and black kings.
There is a total of 32 squares, each having a different index:
| 7 | 28 | 29 | 30 | 31 | ||||
|---|---|---|---|---|---|---|---|---|
| 6 | 24 | 25 | 26 | 27 | ||||
| 5 | 20 | 21 | 22 | 23 | ||||
| 4 | 16 | 17 | 18 | 19 | ||||
| 3 | 12 | 13 | 14 | 15 | ||||
| 2 | 8 | 9 | 10 | 11 | ||||
| 1 | 4 | 5 | 6 | 7 | ||||
| 0 | 0 | 1 | 2 | 3 | ||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Distributed under the MIT License. See LICENSE.md