Algoritma bir problemin çözümü için uygulanması ya da takip edilmesi gereken yönergelerin bütünü olarak ifade edilebilir.

Teknik açıdan bakıldığında ilgili problemin çözümü için kullanılacak komut dizisi de algoritma olarak tanımlanabilir.

Algoritmalar bir probleme karşı sunulan çözüm yolunun adım adım anlatılmasını ve programın karşılaştığı farklı durumlar karşısında kararsız kalmadan sonuca en kısa yoldan ve en az maliyetle gitmesini amaç edinmektedir.

• Her algoritmanın başlangıç ve bitiş noktası vardır. Sonlu adımlar arasında tanımlanırlar. Kimi algoritmalar problemi n adımda çözerken kimi algoritmalar n² adımda çözer.

• Hesaplamalar, veri işleme, otomatik akıl yürütme ve diğer görevleri gerçekleştirmek için algoritmalar özel olarak tanımlanmış sistematik adımları içerir.

✨ Etkili bir algoritma, mevcut donanım kaynaklarını dikkate alarak, sınırlı bir alan ve zaman içinde tanımlı problem için bir çözüm üretebilmelidir.

• Algoritmaların verimli bir şekilde çalışması için çoğu zaman başlangıç koşulları ve ilk girişlerin değerleri belirtilir.

• Algoritma içeriğinde aritmetik ve mantıksal adımlar bulundurabilir. Matematiksel açıdan, algoritmalara bir prosedür ya da fonksiyon gözü ile bakılabilir.

Algoritmaların anlaşılmalarını kolaylaştırmak üzere bir takım bloklar kullanılmaktadır. Bu bloklar bütününe akış şeması denilmektedir.

Şema-1

Şema-1 drawio ile çizilmiştir.

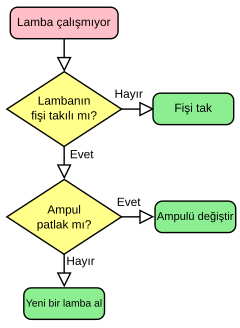
Örnek bir akış şeması inceleyelim.

Şema-2

Şema-2 Örnek akış şeması görseli wikipedia'dan alınmıştır.

İki sayının toplanmasını içeren bir algoritma şeması hazırlayalım.

Şema-3

Şema-3 drawio ile çizilmiştir.

Aylık geliri 5000 lira, aylık gideri 7500 lira olan bir kişinin aylık kâr zarar algoritma şemasını hazırlayalım.

Şema-4

Şema-4 drawio ile çizilmiştir.

Bir temizlik robotunun akış şemasını hazırlayalım.

Şema-5

Şema-5 drawio ile çizilmiştir.

• Programcılar sıklıkla algoritmaları, yalnızca insan gözlerine yönelik bir şekilde tanımlamak isterler.

• Bu tanımlamalar bilgisayar programı ya da bir akış şeması değildir. Daha çok yapılandırılmış bir metin tanımıdır.

• Bu tanımlamalar veri yapısının ya da algoritmanın üst düzey analizini kolaylaştırır.

• Bir kaba kod yazarken bu kodun makinelerin değil, insanların okuyacağı unutulmamalıdır.

• Anlaşılırlık yüksek seviyede tutulmalı, teknik detaylardan kaçınılmalıdır.

Bir örnekle kaba kodu pekiştirelim.

1'den n'e kadar olan sayıları ekrana yazdıran algoritmanın kaba kodlarını yazalım.

Algoritma ekranaYaz(n)
Giriş: Limit değerini temsil eden n sayısı
Çıkış: Değer yok
n değerini oku
i = 0
Koşul belirle i <= n
i ekrana yaz
i'nin değerini 1 arttır
...
ekranaYaz(5)
Başla
i = 0
i <= 5 evet
0

i = 1
i <= 5 evet
1

i = 2
i <= 5 evet
2

i = 3
i <= 5 evet
3

i = 4
i <= 5 evet
4

i = 5
i <= 5 evet
5

i = 6
i <= 5 hayır
5
Son

• Bir değişken bilgisayar hafızasında bir değeri depolamak ve ihtiyaç halinde okumak üzere ayrılmış olan belirli bir yeri ya da alanı işaret eder.

• Bir değişkenin veri türü değişkenin alabileceği, sınırları belirli ve değişken türüne bağlı olarak kendisi için ayrılmış olan alanı gösterir.

• Bir ifade veya bir kod satırı algoritmada izlenecek tek bir adımı tanımlamak üzere kullanılır.

Bir algoritmada temelde üç blok halinde düşünülebilir. Giriş, işleme, çıkış şeklinde özetlenebilir.

• Giriş seti içerisindeki veriler bir ses kaydı, bir imge, bir metin ya da benzer bir ifade olabilir.

• İşleme blogu algoritmaya ait tanımlı prosedürlerin ardışık bir şekilde işlenmesini sağlar.

• Çıkış seti ise verilen girdiye bağlı olarak üretilen çıktıyı temsil eder.

Bir problemin çözümünü sağlamak üzere algoritmanın işlem bileşenleri:

• Atama ifadeleri
• Aritmetik işlemler
• Mantıksal ifadeler
• Döngüler
• Veri yapıları ve organizasyonu
• Yazma ve okuma prosedürleri

• Algoritma prosedürleri işletme şekillerine göre kategorilere ayrılabilirler.

• Bu farklı kategoriler algoritmaların çalışma şekillerine ve yapılarına yansımaktadır.

Şema-6

Şema-6 drawio ile çizilmiştir.

• Direkt Algoritmalar

Algoritmaların en temel çalışma bileşenlerinden biri iterasyonlardır. İterasyon, belirli koşullar altında kendini tekrar eden kod blokları olarak ifade edilebilir. İterasyonlarla çalışmayan algoritmalar direkt algoritmalar olarak isimlendirilir. Örn: ikinci dereceden denklem çözümleri

• Ardışık Algoritmalar

Direkt algoritmaların aksine amaçlanan problemin çözümünü yerine getirmek üzere pek çok algoritma ardışık olarak çalışır ve bu algoritmalar ardışık algoritmalar olarak adlandırılır. Örn: faktöriyel hesapları

• Yakınsak Algoritmalar

Aranılan çözüme doğru yakınsayan ardışık algoritmalardır. Bazı yakınsak algoritmalar kesin çözümü elde edemezler fakat bu çözüme yaklaşık bir değeri kesin çözüm alırlar. Yaklaşık algoritmalar sonlu değillerdir; fakat her bir ileri iterasyon onları kesin çözüme biraz daha yaklaştırır. Yaklaşık algoritmalara değişken kesen metodu, arama teknikleri vb. örnekler verilebilir.

• Sonlu Algoritmalar

İterasyonların sonlu bir sayısında kesin çözümü garanti eden yakınsak algoritmalardır, yol yapılı ve ağaç yapılı olarak ikiye ayrılırlar.

Yol Yapılı algoritmaların pek çoğu yol yapısına sahiptir. Bu yol yapısında bir iterasyon bir önceki iterasyonu iterasyon dizilerinde farklı dallar üretmeksizin takip eder.

Ağaç Yapılı algoritmalar diğer sonlu algoritmalarda iterasyon dizileri, pek çok paralel dalları içeren bir ağaç şeklindedir. Birçok ağaç arama algoritmaları bu sınıfa aittir.