二分查找是一种算法，其输入是一个有序的元素列表（必须有序的原因稍后解释）。如果要 查找的元素包含在列表中，二分查找返回其位置；否则返回null。
class algorithms
{
/// <summary>
/// 二分查找有序列表
/// </summary>
/// <param name="orderList">有序列表</param>
/// <param name="desValue">目标值</param>
/// <returns></returns>
public static int BinarySearch(int[]orderList,int desValue)
{
int low = 0;
int high = orderList.Length - 1;
while (low<=high)
{
int mid = (low + high) / 2;
int guess = orderList[mid];
if (guess == desValue) return mid;
if (guess < desValue)
{
low = mid + 1;
}
else
{
high = mid - 1;
}
}
return -1;
}
}运行时间
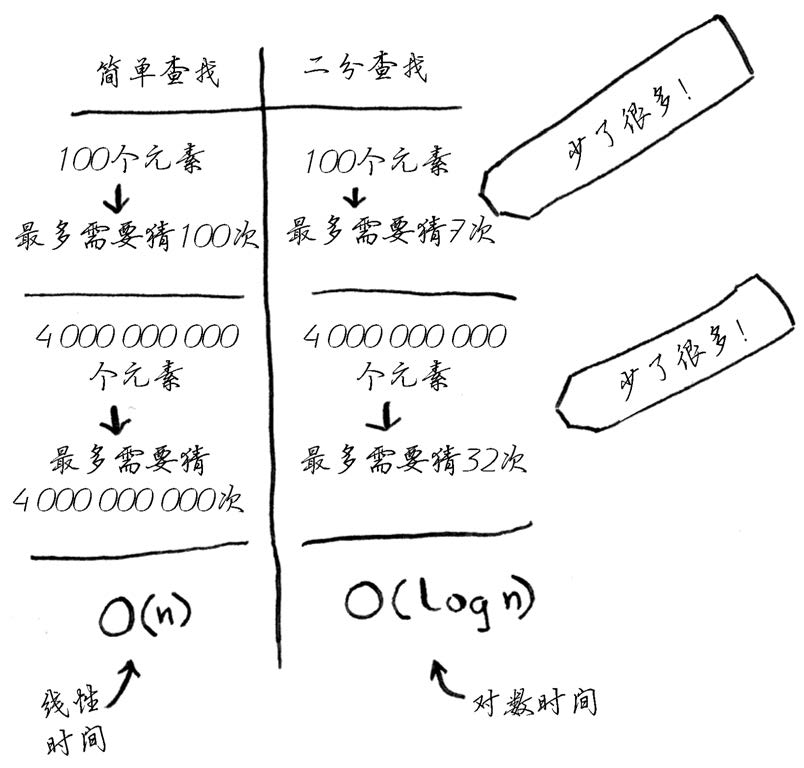
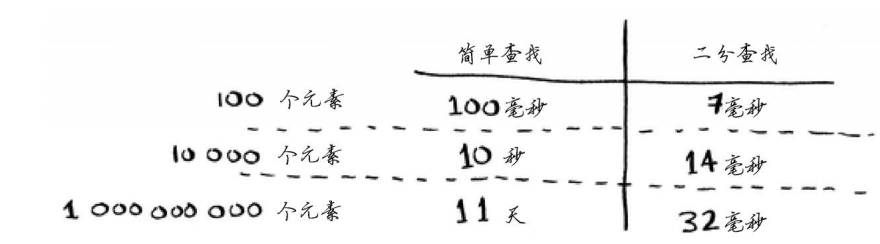
简单查找逐个地检查数字，如果列表包含100个数字，最多需要猜100次。如果列表包含40亿个数字，最多需要猜40亿次。换言之，最多需要猜测的次数与列表长度相同，这被称为线性 时间（ linear time）。
大表示法是一种特殊的表示法，指出了算法的速度有多快。
随着元素数量的增加，二分查找需要的额外时间并不多，而简单查找需要的额外时间却很多。因此，随着列表的增长，二分查找的速度比简单查找快得多。 Bob以为二分查找速度为简单查找的15倍，这不对：列表包含10亿个元素时，为3300万倍。
大表示法指出了算法有多快。例如，假设列表包含
个元素。简单查找需要检查每个元素，因此需要执行次
操作。使用大
表示法，这个运行时间为
。单位秒呢？没有——大表示法
指的并非以秒为单位的速度。 大表示法
让你能够比较操作数，它指出了算法运行时间的增速。
为检查长度为的列表，二分查找需要执行
次操作。大
表示为
下面按从快到慢的顺序列出了你经常会遇到的5种大O运行时间。
-
对数时间，这样的算法包括二分查找；
-
线性时间，这样的算法包括简单查找；
-
这样的算法包括快速排序；
-
这样的算法包括选择排序；
-
这样的算法包括旅行商问题的解决方案。
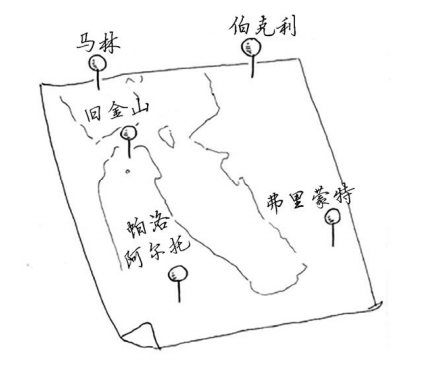
有一位旅行商需要前往5个城市。
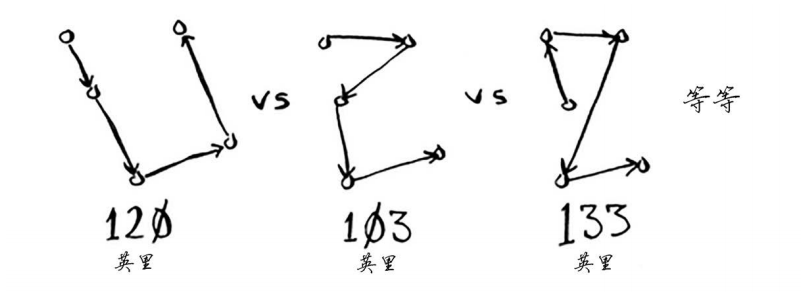
这位旅行商（姑且称之为Opus吧）要前往这5个城市，同时要确保旅程最短。为此，可考虑 前往这些城市的各种可能顺序。
对于每种顺序，他都计算总旅程，再挑选出旅程最短的路线。 5个城市有120种不同的排列方式。因此，在涉及5个城市时，解决这个问题需要执行120次操作。涉及6个城市时，需要执行720次操作（有720种不同的排列方式）。涉及7个城市时，需要执行5040次操作！
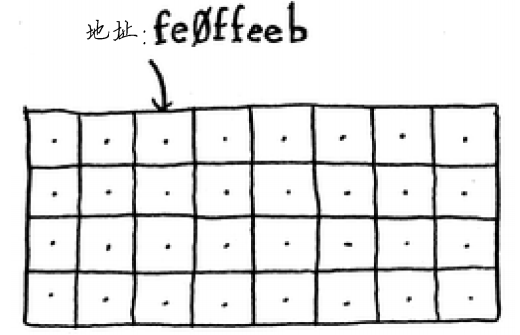
计算机就像是很多抽屉的集合体，每个抽屉都有地址。fe0ffeeb是一个内存单元的地址。
数组与链表操作的运行时间比较
| 数组 | 链表 | |
|---|---|---|
| 读取 | ||
| 插入 | ||
| 删除 |
private static int FindSmallest(int[] iArray)
{
int smallest = iArray[0];
int smallestIndex = 0;
for (int i = 0; i < iArray.Length; i++)
{
if (smallest > iArray[i])
{
smallest = iArray[i];
smallestIndex = i;
}
}
return smallestIndex;
}
private static int[] RemoveListItem(int[] iArray,int index)
{
ArrayList arrayList = new ArrayList();
for (int i = 0; i < iArray.Length; i++)
{
if (i != index)
{
arrayList.Add(Convert.ToInt32(iArray[i]));
}
else continue;
}
int[] newArray = new int[arrayList.Count];
int j = 0;
while (j < newArray.Length)
{
newArray[j] = (int)arrayList[j];
j++;
}
return newArray;
}
//生成新的数组
public static int[] SelectSort(int[] iArray)
{
int[] newArray=new int[iArray.Length];
for (int i = 0; i < newArray.Length; i++)
{
int smallestIndex = FindSmallest(iArray);
newArray[i] = iArray[smallestIndex];
iArray = RemoveListItem(iArray, smallestIndex);
}
return newArray;
}//改变原有数组
public static int[] SelectSortArray(int[] iArray)
{
int temp = 0;
int i = 0;
while (i < iArray.Length - 1)
{
int smallest = iArray[i];
int smallestIndex = i;
for(int j=i+1; j < iArray.Length; j++)
{
if (smallest > iArray[j])
{
smallest = iArray[j];
smallestIndex = j;
}
}
temp = iArray[i];
iArray[smallestIndex] = temp;
iArray[i] = smallest;
i++;
}
return iArray;
}递归就是套娃。
由于递归函数调用自己，因此编写这样的函数时很容易出错，进而导致无限循环。例如，假设你要编写一个像下面这样倒计时的函数。
编写递归函数时，必须告诉它何时停止递归。正因为如此， 每个递归函数都有两部分：基线 条件（ base case）和递归条件（ recursive case） 。递归条件指的是函数调用自己，而基线条件则 指的是函数不再调用自己，从而避免形成无限循环。
栈是一种数据结构，它按照后进先出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据。
public static void CountDown(int number)
{
if (number <= 0) return;
else
{
Console.WriteLine(number);
CountDown(number - 1);
}
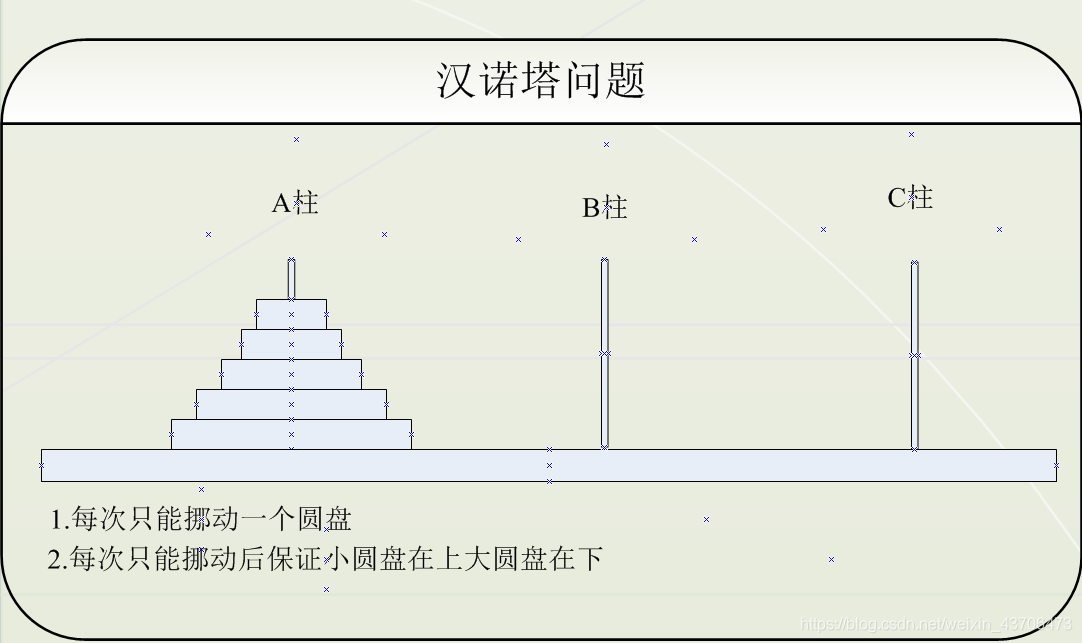
}汉诺塔问题
汉诺塔其实是在1883年的时候有一个法国的数学家名字叫卢卡斯发明的，不过关于这个游戏有一个传说，就是在佛教里面有一个神叫梵天，在创造世界的时候有一个圣地不是叫做贝拿勒斯在这个地方，造一个庙宇，庙宇里面有一个黄铜做的台子上面有三根宝石柱，而在其中一根宝石柱的上面梵天放了六十四个金罗盘，金罗盘上边小下边大，有一个僧侣，在不停的移动的这些金罗盘，而且移动是有规则的，规则是在移动的时候吧，我们每一次只能移动一个，而且这一个就不能放地上，你必须从一个柱子，移动到另外一柱子，不可以两个金罗盘同时移动到同一个柱上，还需要保证每次移动后每根柱子的金罗盘的顺序都是小压大，这个梵天还说，当这个僧侣把六十四个金罗盘都从最左边的柱子挪到最右边柱上的时候，世界就会在一声霹雳中毁灭所有的梵塔庙宇和僧侣也会同归于尽。
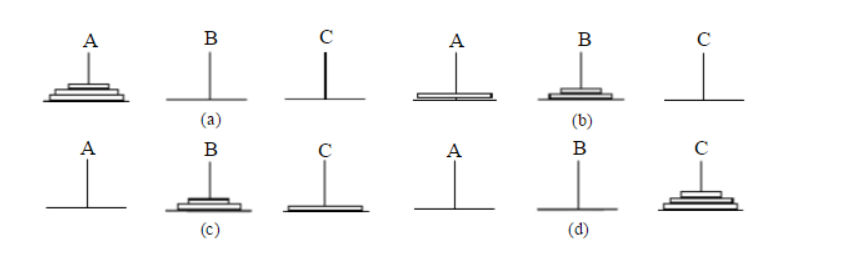
1.当罗盘只有一个的时候只需要把罗盘直接从A柱移动到C组一步就可以完成;
2.当罗盘只有两个的时候需要把小罗盘直接从A柱移动到B组大罗盘移动到C柱然后再将小罗盘移动到C柱三步就可以完成;
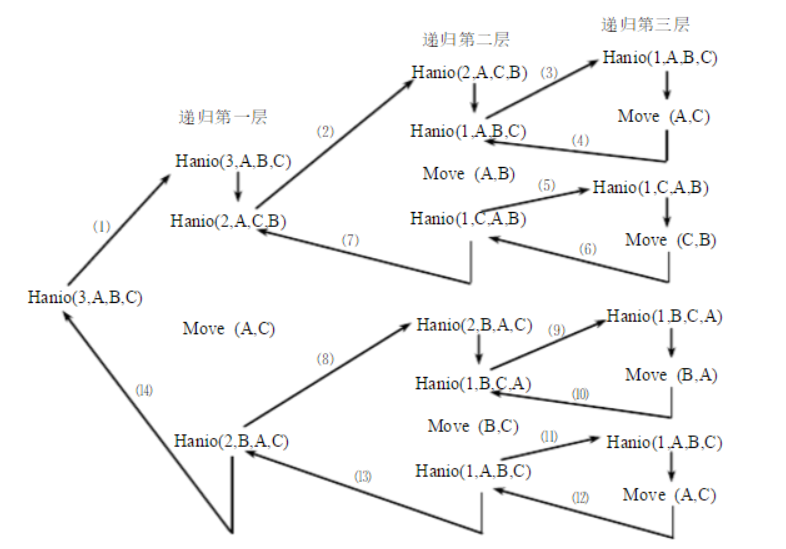
3.当罗盘只有三个我只需要通过某种方法将上面的两片移动到B柱然后再将大罗盘移动到C柱上再把B柱的两个移动到C柱上去就完成了;
4.当罗盘有N个的时候也是通过某种方法将上面的N-1片移动到B柱然后再将大罗盘移动到C柱上再把B柱的N-1移动到C柱上去就完成了，如果想挪N个 那就应该想怎么挪N-1个 ，如果想挪N-1个 那就应该想怎么挪N-1-1个 也以此类推 最终就会变成一个只挪一个圆盘的问题.
